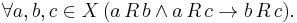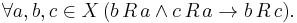Euclidean relation

In mathematics, Euclidean relations are a class of binary relations that satisfy a weakened form of transitivity that formalizes Euclid's "Common Notion 1" in The Elements: things which equal the same thing also equal one another.

Definition

A binary relation R on a set X is Euclidean (sometimes called right Euclidean) if it satisfies the following: for every a, b, c in X, if a is related to b and c, then b is related to c.^[1]

To write this in predicate logic:

$\forall a, b, c\in X\,(a\,R\, b \land a \,R\, c \to b \,R\, c).$

Dually, a relation R on X is left Euclidean if for every a, b, c in X, if b is related to a and c is related to a, then b is related to c:

$\forall a, b, c\in X\,(b\,R\, a \land c \,R\, a \to b \,R\, c).$

Relation to transitivity

The property of being Euclidean is different from transitivity: both the Euclidean property and transitivity infer a relation between b and c from relations between a and b and between a and c, but with different argument orderings in the relations. However, if a relation is symmetric, then the argument orders do not matter, so in this case it is Euclidean if and only if it is transitive.^[1]

If a relation is Euclidean and reflexive, it must also be symmetric and transitive, and hence it must be an equivalence relation. Consequently, equivalence relations are exactly the reflexive Euclidean relations.^[1]

References

^ ^a ^b ^c Fagin, Ronald (2003), Reasoning About Knowledge, MIT Press, p. 60, ISBN 9780262562003, http://books.google.com/books?id=xHmlRamoszMC&pg=PA60 .